Hi, Sam-
Apologies for the belated reply.
I am not sure what cosine regressors were used? For example, one can use cosine regressors to mirror FFT-like bandpassing, but that depends on which frequencies were used and how they were set up.
You can check the FFT of a time series with 3dDFT (NB: 3dFFT does a spatial Fourier Transform; DFT = discrete Fourier Transform, across time at each element). For example, with the AFNI_demos/FATCAT_DEMO data, I can run the following on 0.01-0.1 Hz bandpassed resting state dataset:
3dDFT -prefix dft -abs REST_in_DWI.nii.gz
... to get a new time series of the FT magnitude values (magnitude = sqrt(power)). There are 195 time points in this particular time series, so there will be 195 FT magnitudes, with some fun aspects: the [0]th should be the mean of the dataset, which is often muuuch larger than the other frequency magnitudes. And there are only ~N/2 independent FT magnitudes---from 0 to the Nyquist frequency are the mirror image of the next N/2. So, to view just the independent set and to skip over the super-large mean value (which might be smeared over the first couple magnitudes), one open up the following in the GUI:
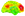
afni dft+orig'[2..97]'
... which looks like the attached. Note how the lower frequencies (left side of the plot, since the abscissa here is frequency) have nonzero magnitudes, while the larger ones (from 0.1 to Nyquist, actually) have zero magnitudes. That is one way I know that this data has been bandpassed.
I *could* run this through 3dRSFC now. *But* the fALFF values would be meaningless. The ALFF values, if I ask for htem within the non-bandpassed range, should be approximately the same as what they would be if I calculated from the not-already-bandpassed data (there is probably a bit of rounding/tapering difference, which should be minimal). The fALFF can't be calculated, because that is the ratio of the sum of the LFF magnitudes to the sum of all magnitudes (not including baseline)---since they higher frequencies have been removed, that is unfair to now ask. So, it really depends what you want to estimate.
I think doing what you suggest:
3dRSFC -prefix RSFC 0.008 0.1 -input data.nii.gz -nodetrend -ort f.1D
makes sense and should be done appropriately. But are you sure you don't want to detrend?
The processing should be done correctly (from 3dRSFC's help):
* The order of processing steps is the following (most are optional), and
for the LFFs, the bandpass is done between the specified fbot and ftop,
while for the `whole spectrum' (i.e., fALFF denominator) the bandpass is:
done only to exclude the time series mean and the Nyquist frequency:
(0) Check time series for initial transients [does not alter data]
(1) Despiking of each time series
(2) Removal of a constant+linear+quadratic trend in each time series
(3) Bandpass of data time series
(4) Bandpass of -ort time series, then detrending of data
with respect to the -ort time series
(5) Bandpass and de-orting of the -dsort dataset,
then detrending of the data with respect to -dsort
(6) Blurring inside the mask [might be slow]
(7) Local PV calculation [WILL be slow!]
(8) L2 normalization [will be fast.]
(9) Calculate spectrum and amplitudes, for RSFC parameters.
3dRSFC is not made to handle censoring. I don't think that can be done here with the ort regressors, because the regressors get bandpassed before application. 3dRSFC is made for non-censored time series.
3dLombScargle (with 3dAmpToRSFC) is the program to take censored data (or data+censoring information) and estimate a power spectrum for RSFC parameters. That one doesn't take orts---the assumption is that you have already processed your data.
In general, one is in a bit of a quandary with bandpassing during processing and later estimating RSFC params, if one wants fALFF.
--pt
Attachments:
open |
download -
fft_of_bandpassed_resting_data.png
(13.1 KB)