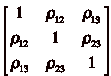-27-
Further
Directions for Group Analysis Research and Software
•In a mixed
effects model, ANOVA cannot deal with unequal variances in the random factor between
different levels of a fixed factor
HExample: 2-way layout, factor A=stimulus type (fixed
effect), factor B=subject (random effect)
Ś As seen earlier,
ANOVA can detect differences in means between levels in A (different
stimuli)
ŚBut if the measurements from different stimuli also have
significantly different variances (e.g., more attentional wandering in
one task vs. another), then the ANOVA model for the signal is wrong
ŚIn general, this “heteroscedasticity” problem is a difficult one,
even in a 2-sample t-test; there is no exact F- or t-statistic
to test when the means and the variances might differ simultaneously
•Although ANOVA
does allow somewhat for intra-subject correlations in measurements, it
is not fully general
HExample: 2-way layout as above, 3 stimulus types in factor
A; general
correlation
matrix between the 3 different types of responses is
but
ANOVA only properly deals with the
case r12=r13=r23
(recall
we are assuming subject effects are random; this is the
correlation
matrix for the intra-subject random responses).
•Possible
solution: general linear-quadratic minimum variance mixed effects modeling
HA
statistical theory not yet much applied to FMRI data (but it will be,
someday)
HQuestions of sample size (number of subjects needed) will surely
arise